- FRACHTBERECHNUNG ZUR BEURTEILUNG DER GEWÄSSERGÜTE • ORIGINALARBEIT
- Published:
Analyse „stetigkeitsbasierter“ Methoden zur Bestimmung von Stofffrachten in Fließgewässern
Analysis of “continuity-based” methods for load calculation in bodies of flowing water
Environmental Sciences Europe volume 21, pages 527–538 (2009)
Zusammenfassung
Ziel und Hintergrund
Mit wachsendem Umweltbewusstsein rückt auch die Frachtberechnung als ein wichtiges Hilfsmittel zur Beurteilung der Gewässergüte weiter in den Vordergrund. Um so mehr ist es wünschenswert, für die jeweilige Situation aufgrund der vorhandenen Datenbasis das beste Verfahren zur Bestimmung von Stofffrachten zu finden. Es werden Kriterien erarbeitet, um diese Vorgabe zu erreichen.
Methode
Die Fracht eines Wasserinhaltsstoffes ist eine integrale Größe von zeitkontinuierlichen Transportwerten (Produkt von Konzentration und Abfluss) über einen bestimmten Zeitraum, beispielsweise ein Jahr (Jahresfracht). Da die üblicherweise zur Verfügung stehenden Daten jedoch nur eine Stichprobe im Sinne der Statistik darstellen und somit das Ergebnis der Frachtbestimmung variieren kann, je nach dem, welche Beobachtungen konkret vorliegen, ist der berechnete Wert als eine Schätzung für die Fracht anzusehen, der mit einer Unsicherheit behaftet ist. Diese durch die Stichprobe induzierte Unsicherheit wird quantifiziert, indem Varianz (Streuung um den „erwarteten“ Wert) plus Quadrat der Verzerrung (Abweichung des „erwarteten“ Wertes vom wahren Wert) zumindest näherungsweise ermittelt wird. Sie heißt mittlerer quadratischer Fehler. Die methodischen Ergebnisse werden durch Beispiele illustriert.
Schwerpunkt
Das Hauptaugenmerk liegt auf den Verfahren, die neben den zeitdiskret beobachteten Konzentrationsdaten auf quasi-kontinuierliche Aufzeichnungen von weiteren Einflussgrößen, insbesondere dem Abfluss, zurückgreifen können. Dazu werden mathematisch-statistische Modelle entwickelt, die Fracht abgeleitet und aufgrund der vorliegenden Daten geschätzt. Dabei zeigt sich, dass alle Modellschätzformeln auf die übliche Stichprobenformel zurückführbar sind, zuzüglich von Termen, die aus dem Vergleich bestimmter Maßzahlen (z. B. Mittelwert) der quasi-kontinuierlichen und der diskreten Stichprobenwerte hervorgehen. Die Stichprobenformel wird in dieser Weise „stetigkeitskorrigiert“. Diese Methodik heißt „stetigkeitsbasierte“ Frachtbestimmung.
Ergebnisse
Überraschenderweise zeigt sich, dass für die Frachtberechnung allein keine komplexen mathematisch-statistischen Modelle erforderlich sind. Das einfache lineare Konzentrations- oder Transportabflussmodell genügt bereits. Die Hinzunahme weiterer Einflussgrößen führt meist zu einem größeren mittlerem quadratischen Fehler in der Frachtschätzung, obwohl die Modellanpassung an die Daten nicht schlechter werden kann. Nur perfekte Modelle, die die Konzentration nahezu exakt beschreiben, führen zu einem kleineren Fehler.
Schlussfolgerungen
Zur Frachtberechnung genügt die Verwendung einer der angegeben Formeln mit einer „Stetigkeitskorrektur“, was ohne die Verwendung eines Software-Programms möglich ist.
Abstract
Aim and background
Increasing ecological awareness puts the load as a tool for water quality assessment in the foreground. Therefore it is very desirable to find optimal procedures for any given situation on basis of existing data. Criteria will be derived to fill that desire.
Method
The load for a water ingredient is an integrated entity of time-continuous loads (product of concentration and flow) for a given time, i. e. a year (yearly load). Normally you can only observe a sample (in a statistical meaning) of these data. Therefore, load calculations vary with the concrete sample given. Each such calculation represents an estimation of the load, afflicted with some uncertainty. This uncertainty can be quantified, at least approximatively, by adding variance (scatter around “expected” mean) and the square of bias (divergence of “expected” mean from true mean). This quantity is called “mean squared error”. The methodological results will be illustrated by examples.
Focus
The main focus lies on the methodologies, which, besides data of concentrations observed discretely in time, additionally use quasi-continuously recorded data of other variates, namely the flow. For that situation, statistical models are developed and the load derived and estimated according to existing data. Hereby it is seen that all model based estimation formulae can be described as standard sampling formulae plus some additional terms which stem from comparison of some measurements (i.e. mean) for quasi-continuous and discrete samples. This way a “continuity-correction” is performed on the standard formulae for the sampling case. This method is called “continuity-based” load determination.
Results
A surprising result is that no complicated mathematical-statistical models are necessary to determine the load. A simple linear concentration- or load-flow-model is sufficient. Additional variates lead, most of the time, to a larger mean squared error in load estimation, even when it is well known that they cannot detoriate the model fit. Only models which describe the concentration extraordinarily precise, near perfection, result in a smaller error.
Implications
It is enough to use one of the given formulae with some “continuity correction” to calculate a load. That can be done without using any software.
1 Einleitung
In den nationalen und internationalen Forschungsbemühungen im Umwelt- und insbesondere im Gewässerschutz, dokumentiert durch vielfältige Zielvorgaben und Auftragsstudien, stellt die Bestimmung von Stofffrachten in Fließgewässern einen wichtigen Bestandteil zur Überwachung des Schadstoffeintrags dar. Umfassender und allgemeiner Art sind beispielsweise das vom Bundesministerium für Bildung und Forschung (BMBF) geförderte, aus 13 Teilen bestehende Projekt Sediment Dynamics and Pollutant Mobility in Rivers (SEDYMO), siehe Förstner und Westrich (2005) und Westrich und Förstner (2005), das sich also schwerpunktmäßig mit der Feinsedimentdynamik und Schadstoffmobilität in Fließgewässern befasst. Ferner gibt es zahlreiche Beiträge im Zusammenhang mit der EU-Wasserrahmenrichtlinie (BMU 2004, 2005), etwa Fehr (2000) zum Thema Nährstoffbilanzen für Flusseinzugsgebiete oder Trepel und Kluge (2002) zur Eignung von Modellen für deren Umsetzung, um nur einige neuere Forschungsarbeiten zu nennen.
Teilweise bzw. überwiegend dem Thema Frachtberechnung widmen sich das Projekt von Richards (1998), der Beitrag von Brunswig (2000), die OSPAR-Pilotstudie von Heininger und Schild (2002) und das mehrjährige Vorhaben von Gölz und Schmidt (2003). Während in den meisten Berichten bekannte Verfahren zur Frachtberechnung zur Anwendung kommen, empfiehlt Brunswig sein Simulationsmodell TRANSPOS für diese Aufgabe. Daneben gibt es weitere Arbeiten in diesem Bereich, wie etwa die von Klopp (1986), Steinebach (1994), Keller et al. (1997), Schreiber und Krauß-Kalweit (1999) oder Hilden (2003), die aufgrund praktischer Erfahrungen und empirischer Beispielrechnungen Empfehlungen zur Frachtberechnung ableiten.
Probabilistische Ansätze im Zusammenhang mit einem regionalen Modell zu Konzentration und Abfluss diskutieren beispielsweise Warn und Brew (1980) und DiToro (1984). Dem Autor ist jedoch keine Arbeit bekannt, die bei Frachtberechnungen versucht, den Stichprobenfehler mathematisch-statistisch zu quantifizieren, um zu objektiven Beurteilungen zu kommen. Das könnte daran liegen, dass die Theorie trotz der einfachen Fragestellung klassische Wege verlässt. Üblicherweise liegt eine zeitäquidistante Auswahl der Beobachtungszeitpunkte vor. Der erste Zeitpunkt ist im Prinzip rein zufällig gewählt und die weiteren Zeitpunkte werden im festen Abstand vorgegeben. Also sind im statistischen Sinne alle Zeitpunkte zufällig und zudem abhängig voneinander. Die bei diesem Zeitstichprobenplan zu realisierenden Messgrößenwerte sind dann ebenfalls als zufällig, abhängig und auch als nichtstationär anzusehen, siehe Hebbel (2006). In dieser Form gehen sie als Einflussgrößen in die mathematisch-statistischen Modelle ein. Damit kann nicht mehr die Modelltheorie mit festen Regressoren und besten linearen unverzerrten Schätzern herangezogen werden. Die Schätzer sind infolge zufälliger Einflussgrößen vielmehr nichtlinear und verzerrt. Um dennoch die Herleitung der Ergebnisse verständlich zu machen, bedarf es einiger mathematischer Begriffsbestimmungen. Eine Vertiefung in die Theorie ist in Hebbel (2006) und Hebbel und Steuer (2007) zu finden.
2 Zeitintervallmaßzahlen von Messgrößen
Auf einem vorgegebenen Zeitintervall J von Zeitpunkt  bis
bis  und damit der Länge
und damit der Länge  werden verschiedene Messgrößen X, Y usw. im Zeitverlauf betrachtet, insbesondere der Abfluss Q und die (querschnittsgemittelte) Konzentration eines Wasserinhaltsstoffes C an einem Fließquerschnitt. Die theoretischen Werte zu einem Zeitpunkt t aus J sind dann
werden verschiedene Messgrößen X, Y usw. im Zeitverlauf betrachtet, insbesondere der Abfluss Q und die (querschnittsgemittelte) Konzentration eines Wasserinhaltsstoffes C an einem Fließquerschnitt. Die theoretischen Werte zu einem Zeitpunkt t aus J sind dann  usw. Konkret ermittelte Werte zu ausgewählten Messzeitpunkten
usw. Konkret ermittelte Werte zu ausgewählten Messzeitpunkten  aus J werden bezeichnet mit
aus J werden bezeichnet mit  usw.
usw.
Der theoretische bzw. empirische Intervallmittelwert der Messgröße X ist der theoretische bzw. empirische (arithmetische) Mittelwert im Zeitintervall J, gegeben durch

z. B. Jahresmittel, Tagesmittel, Stundenmittel, je nach Wahl von J.
Die theoretische bzw. empirische Intervallvarianz der Messgröße X ist die theoretische bzw. empirische mittlere quadratische Abweichung vom entsprechenden Intervallmittelwert im Zeitintervall J, gegeben durch

Die theoretische bzw. empirische Intervallkovarianz der Messgrößen X und Y im Zeitintervall J ist definiert durch

bzw.

mit der multiplikativen Größe  und stellt ein Maß für ihren theoretischen bzw. empirischen linearen Zusammenhang in J dar.
und stellt ein Maß für ihren theoretischen bzw. empirischen linearen Zusammenhang in J dar.
Die theoretische bzw. empirische Intervallkorrelation der Messgrößen X und Y im Zeitintervall J ist ein auf den Bereich −1 bis 1 normiertes Maß für ihren theoretischen bzw. empirischen linearen Zusammenhang in J, gegeben durch  .
.
Diese Intervallmaßzahl gibt an, wie gut die Werte  bzw.
bzw.  in J auf einer Modellgeraden der Art
in J auf einer Modellgeraden der Art

liegen. Dabei wird Y zurückgeführt auf einen in X linearen Teil und in einen Restteil (als Differenzgröße). Werden die Gleichungen nach  bzw.
bzw.  aufgelöst und ihre Intervallvarianzen berechnet, ergibt sich unmittelbar
aufgelöst und ihre Intervallvarianzen berechnet, ergibt sich unmittelbar  bzw.
bzw.  . Für
. Für  , d. h.
, d. h.  bzw.
bzw.  , d. h.
, d. h.  ist die Gerade positiv (negativ) geneigt und die Abweichungen
ist die Gerade positiv (negativ) geneigt und die Abweichungen  bzw.
bzw.  sind identisch Null im betrachteten Intervall, da in diesem Fall
sind identisch Null im betrachteten Intervall, da in diesem Fall  bzw.
bzw.  ist. Für
ist. Für  bzw.
bzw.  , also
, also  bzw.
bzw.  spielt der lineare Teil im Modell keine Rolle. In diesem Fall heißen X und Y theoretisch bzw. empirisch intervallunkorreliert oder linear unabhängig im Zeitintervall J.
spielt der lineare Teil im Modell keine Rolle. In diesem Fall heißen X und Y theoretisch bzw. empirisch intervallunkorreliert oder linear unabhängig im Zeitintervall J.
Die Intervallkorrelation der Ganglinien  und
und  im Intervall J hängt danach sowohl von ihren Funktionstypen (in t) als auch vom betrachteten Intervall J ab, aus dem t stammt. Ist speziell eine der zentrierten Funktionen
im Intervall J hängt danach sowohl von ihren Funktionstypen (in t) als auch vom betrachteten Intervall J ab, aus dem t stammt. Ist speziell eine der zentrierten Funktionen  bezüglich der Intervallmitte von J gerade und die andere ungerade, so ist ihr Produkt ungerade und damit das Integral bzw.
bezüglich der Intervallmitte von J gerade und die andere ungerade, so ist ihr Produkt ungerade und damit das Integral bzw.  gleich Null. Im
gleich Null. Im  -Diagramm bilden in diesem Fall die Punktepaare
-Diagramm bilden in diesem Fall die Punktepaare  vom Intervallanfang (
vom Intervallanfang ( ) bis Intervallende (
) bis Intervallende ( ) einen Weg, der „symmetrisch“ zum Mittelpunkt
) einen Weg, der „symmetrisch“ zum Mittelpunkt  verläuft. Eine bestimmte positiv oder negativ geneigte Richtung des Gesamtweges ist nicht erkennbar.
verläuft. Eine bestimmte positiv oder negativ geneigte Richtung des Gesamtweges ist nicht erkennbar.
Beispielsweise liegen für die ungeraden bzw. geraden Funktionen  die Punktepaare
die Punktepaare  wegen
wegen  für t von 0 bis
für t von 0 bis  auf einem Kreis mit Radius Eins. Eine bestimmte Richtung ist auf dem Gesamtweg längs des Kreises von 0 bis
auf einem Kreis mit Radius Eins. Eine bestimmte Richtung ist auf dem Gesamtweg längs des Kreises von 0 bis  nicht vorherrschend. Die Intervallkovarianz ist Null. Hingegen wäre für ein kleines Teilintervall der Weg ein Teilstück auf dem Kreis und dieser hätte (je nach Ausschnitt) eine überwiegend positive oder negative Richtung und
nicht vorherrschend. Die Intervallkovarianz ist Null. Hingegen wäre für ein kleines Teilintervall der Weg ein Teilstück auf dem Kreis und dieser hätte (je nach Ausschnitt) eine überwiegend positive oder negative Richtung und  wäre ungleich Null.
wäre ungleich Null.
3 Abfluss, Konzentration, Transport und Fracht
Der Abfluss (Durchfluss) an einem Fließquerschnitt zum Zeitpunkt t ist das Wasservolumen, das sich pro Zeiteinheit dort hindurch bewegt (z. B. in m3/s).
Die (Massen-)Konzentration eines Wasserinhaltsstoffes C an einem Fließquerschnitt zum Zeitpunkt t ist die dort mittlere Konzentration zum Zeitpunkt t, (z. B. in mg/l  g/m3). Im Folgenden wird abkürzend von der Konzentration
g/m3). Im Folgenden wird abkürzend von der Konzentration  gesprochen. Zur möglichst genauen empirischen Bestimmung von
gesprochen. Zur möglichst genauen empirischen Bestimmung von  sind entweder viele Messungen im Querschnitt erforderlich oder es muss aufgrund der Erfahrung eine „repräsentative“ Stelle im Querschnitt ausgewählt werden. Davon wird hier stets ausgegangen.
sind entweder viele Messungen im Querschnitt erforderlich oder es muss aufgrund der Erfahrung eine „repräsentative“ Stelle im Querschnitt ausgewählt werden. Davon wird hier stets ausgegangen.
Der Transport zum Zeitpunkt t ist die pro Zeiteinheit durch den Fließquerschnitt bewegte Masse eines Stoffes, also (näherungsweise)
zum Zeitpunkt t ist die pro Zeiteinheit durch den Fließquerschnitt bewegte Masse eines Stoffes, also (näherungsweise)

Die FrachtF im Zeitintervall J der Länge  (z. B. in s) ist die in dieser Zeitspanne insgesamt durch den Fließquerschnitt bewegte Masse eines Stoffes, also
(z. B. in s) ist die in dieser Zeitspanne insgesamt durch den Fließquerschnitt bewegte Masse eines Stoffes, also

Es ist zweckmäßig, eine weitere Größe einzuführen, die im Zusammenhang mit der Fracht F steht. Sie wird hier MischprobenfrachtM im Zeitintervall J (z. B. in s) genannt und ist das auf J hochgerechnete Produkt der Intervallmittelwerte  und
und  , also
, also

Der Name Mischprobenfracht wird gewählt, weil im Prinzip der Intervallmittelwert  über eine kontinuierliche zeitproportionale Mischprobe gewonnen werden kann, wenn der Stoff „probenstabil“ ist und keine Konservierungsprobleme auftreten. Bei „quasi-kontinuierlich“ erfasstem Abfluss lässt sich auch
über eine kontinuierliche zeitproportionale Mischprobe gewonnen werden kann, wenn der Stoff „probenstabil“ ist und keine Konservierungsprobleme auftreten. Bei „quasi-kontinuierlich“ erfasstem Abfluss lässt sich auch  sehr genau berechnen, so dass M in diesem Fall leicht und fast fehlerfrei ermittelt werden kann.
sehr genau berechnen, so dass M in diesem Fall leicht und fast fehlerfrei ermittelt werden kann.
Wesentlich für die weiteren Untersuchungen ist der Zusammenhang der Fracht F und der Mischprobenfracht M. Nach Definition der Intervallkovarianz  ergibt sich unmittelbar die folgende Aussage:
ergibt sich unmittelbar die folgende Aussage:
Für die Fracht F und die Mischprobenfracht M gilt nach Definition der Intervallkovarianz  die Fundamentalgleichung
die Fundamentalgleichung

d. h. F und M stimmen dann und nur dann überein, wenn  , also wenn C und Q im Intervall unkorreliert sind, wie am Ende von Kap. 1 beschrieben. Insbesondere führt ein Zusammenhang der Art
, also wenn C und Q im Intervall unkorreliert sind, wie am Ende von Kap. 1 beschrieben. Insbesondere führt ein Zusammenhang der Art  nicht automatisch zur Unkorreliertheit von C und Q im Intervall J, weil dann
nicht automatisch zur Unkorreliertheit von C und Q im Intervall J, weil dann  ist. Es müssten also
ist. Es müssten also  und
und  im Intervall J unkorreliert sein und das trifft auch nur für bestimmte Funktionstypen und Intervalle zu (z. B.
im Intervall J unkorreliert sein und das trifft auch nur für bestimmte Funktionstypen und Intervalle zu (z. B.  ungerade in Bezug zur Intervallmitte).
ungerade in Bezug zur Intervallmitte).
4 Strategien zur Frachtermittlung
In der Praxis werden zur Frachtbestimmung und dabei speziell zur Gewinnung der Konzentrationsdaten im Wesentlichen die Mischprobenstrategie und die systematische Zeitstichprobe zugrunde gelegt.
4.1 Mischprobenstrategie
Bei der Mischprobenstrategie wird das Gesamtintervall J in Teilintervalle  eingeteilt, in die sogenannten Messintervalle, die üblicherweise gleich groß gewählt werden. In den Messintervallen wird dem Fließgewässer jeweils eine (zeitproportionale) Mischprobe entnommen, d. h. in kleinen zeitlichen äquidistanten Abständen innerhalb eines Messintervalls werden Wasserproben gleichen Volumens entnommen und zu einer gemeinsamen Probe vereinigt. Dieses Vorgehen heißt Mischprobenstrategie. Von der praktischen Probennahme über die chemische Analytik bis hin zur Aufzeichnung des Zahlenergebnisses können eine Vielzahl von Fehlern auftreten, die hier sämtlich unberücksichtigt bleiben. Das Resultat ist rein theoretisch jeweils der Intervallmittelwert
eingeteilt, in die sogenannten Messintervalle, die üblicherweise gleich groß gewählt werden. In den Messintervallen wird dem Fließgewässer jeweils eine (zeitproportionale) Mischprobe entnommen, d. h. in kleinen zeitlichen äquidistanten Abständen innerhalb eines Messintervalls werden Wasserproben gleichen Volumens entnommen und zu einer gemeinsamen Probe vereinigt. Dieses Vorgehen heißt Mischprobenstrategie. Von der praktischen Probennahme über die chemische Analytik bis hin zur Aufzeichnung des Zahlenergebnisses können eine Vielzahl von Fehlern auftreten, die hier sämtlich unberücksichtigt bleiben. Das Resultat ist rein theoretisch jeweils der Intervallmittelwert  eines Messintervalls
eines Messintervalls  . Weitere Voraussetzung ist, dass die Abflussdaten
. Weitere Voraussetzung ist, dass die Abflussdaten  „quasi-kontinuierlich“ vorliegen bzw. jeweils der Intervallmittelwert
„quasi-kontinuierlich“ vorliegen bzw. jeweils der Intervallmittelwert  eines Messintervalls bekannt ist. Damit kann jeweils die Mischprobenfracht
eines Messintervalls bekannt ist. Damit kann jeweils die Mischprobenfracht  berechnet werden. Der Wert
berechnet werden. Der Wert

heißt Frachtschätzung nach der Mischprobenstrategie. Er stimmt aber nicht mit der eigentlich gesuchten Fracht F überein, er ist verzerrt. Aufgrund der jeweiligen Frachtfundamentalgleichung  nach Kap. 3 mit der Intervallkovarianz
nach Kap. 3 mit der Intervallkovarianz  im Teilintervall
im Teilintervall  sowie
sowie  ergibt sich der Zusammenhang
ergibt sich der Zusammenhang

wobei  als interne und
als interne und  als externe Intervallkovarianz bezeichnet werden, die sich zu
als externe Intervallkovarianz bezeichnet werden, die sich zu  ergänzen. Der mittlere quadratische Fehler der Schätzung
ergänzen. Der mittlere quadratische Fehler der Schätzung  für F ist durch das Verzerrungsquadrat
für F ist durch das Verzerrungsquadrat  gegeben.
gegeben.
Allgemein gelten bei positiven (internen und externen) linearen C–Q-Zusammenhängen (Ausschwemmungseffekte) die Relationen

und entsprechend bei negativen (internen und externen) linearen C–Q-Zusammenhängen (Verdünnungseffekte)

Unterschiedliche Relationen, also  oder
oder  sind zwar möglich, treten jedoch in der Praxis seltener auf.
sind zwar möglich, treten jedoch in der Praxis seltener auf.
Je kleiner die Teilintervalle  gewählt werden, desto kleiner ist im Allgemeinen auch die Verzerrung, weil dann mindestens eine der Größen C oder Q dort als konstant angesehen werden kann, d. h.
gewählt werden, desto kleiner ist im Allgemeinen auch die Verzerrung, weil dann mindestens eine der Größen C oder Q dort als konstant angesehen werden kann, d. h.  ist, vgl. Abschn. 4.3.
ist, vgl. Abschn. 4.3.
Auch bei größeren Teilintervallen  stimmt die Frachtschätzung
stimmt die Frachtschätzung  mit der Fracht F dann überein, wenn sich im Mittel die einzelnen Messintervallkovarianzen
mit der Fracht F dann überein, wenn sich im Mittel die einzelnen Messintervallkovarianzen  aufheben, also wenn die interne Intervallkovarianz verschwindet. Zur Ermittlung von Jahresfrachten erweisen sich in etlichen praktischen Fällen 7- oder 14-tägige Mischproben als geeignet, da der interne lineare Zusammenhang von C und Q und damit die Verzerrung relativ gering ist (vgl. Schreiber und Krauß-Kalweit 1999; Hebbel und Steuer 2007). Da aber vor der Anwendung dieser Strategie kaum bekannt sein wird, ob
aufheben, also wenn die interne Intervallkovarianz verschwindet. Zur Ermittlung von Jahresfrachten erweisen sich in etlichen praktischen Fällen 7- oder 14-tägige Mischproben als geeignet, da der interne lineare Zusammenhang von C und Q und damit die Verzerrung relativ gering ist (vgl. Schreiber und Krauß-Kalweit 1999; Hebbel und Steuer 2007). Da aber vor der Anwendung dieser Strategie kaum bekannt sein wird, ob  ist, kann die Verzerrung nicht abgeschätzt werden. Auch nachher ist es ohne zusätzliche Informationen nicht möglich, den Fehler zu quantifizieren und ggf. zu korrigieren, da jeweils nur ein Wertepaar
ist, kann die Verzerrung nicht abgeschätzt werden. Auch nachher ist es ohne zusätzliche Informationen nicht möglich, den Fehler zu quantifizieren und ggf. zu korrigieren, da jeweils nur ein Wertepaar  , in einem Teilintervall vorliegt, aus dem die einzelne Kovarianz
, in einem Teilintervall vorliegt, aus dem die einzelne Kovarianz  nicht sinnvoll geschätzt werden kann.
nicht sinnvoll geschätzt werden kann.
Zusammenfassung Der Mischprobenschätzer  ist rein mathematisch-statistisch gesehen immer dann gut, wenn der mittlere lineare Zusammenhang von C und Q in den Probenintervallen gering ist. In vielen praktischen Fällen ist diese Voraussetzung zutreffend.
ist rein mathematisch-statistisch gesehen immer dann gut, wenn der mittlere lineare Zusammenhang von C und Q in den Probenintervallen gering ist. In vielen praktischen Fällen ist diese Voraussetzung zutreffend.
4.2 Stichprobenstrategie
Werden zu einzelnen ausgewählten Zeitpunkten  aus „repräsentativen“ Messintervallen
aus „repräsentativen“ Messintervallen  die eine Zerlegung des Gesamtintervalls J darstellen, Wasserproben entnommen und analysiert, dann liegt eine Stichprobenstrategie vor. Die Zeitpunkte bzw. Messintervalle werden als repräsentativ angesehen, wenn
die eine Zerlegung des Gesamtintervalls J darstellen, Wasserproben entnommen und analysiert, dann liegt eine Stichprobenstrategie vor. Die Zeitpunkte bzw. Messintervalle werden als repräsentativ angesehen, wenn  gilt. Dann ist die Frachtschätzung durch
gilt. Dann ist die Frachtschätzung durch

recht genau für die Fracht  . Um diese näherungsweise Gleichheit zu erreichen, insbesondere bei größeren Teilintervallen, müssten im Prinzip Konzentration und Abfluss ständig beobachtet werden. Die praktische Umsetzung einer derartigen sogenannten bewussten Auswahl wäre sehr personal- und zeitaufwändig sowie stoffabhängig (einerseits wegen unterschiedlicher Dynamiken und andererseits aus chemisch-analytischen Gründen). Daher wird die bewusste Auswahl im Allgemeinen nicht realisierbar sein und hier nicht weiter verfolgt. Außerdem ließe sich der statistische Fehler nicht abschätzen.
. Um diese näherungsweise Gleichheit zu erreichen, insbesondere bei größeren Teilintervallen, müssten im Prinzip Konzentration und Abfluss ständig beobachtet werden. Die praktische Umsetzung einer derartigen sogenannten bewussten Auswahl wäre sehr personal- und zeitaufwändig sowie stoffabhängig (einerseits wegen unterschiedlicher Dynamiken und andererseits aus chemisch-analytischen Gründen). Daher wird die bewusste Auswahl im Allgemeinen nicht realisierbar sein und hier nicht weiter verfolgt. Außerdem ließe sich der statistische Fehler nicht abschätzen.
Realistisch gesehen sind die Beobachtungszeitpunkte mehr oder weniger zufällig festgelegt. Sind sie nach einer rein zufälligen Zeitstichprobe ausgewählt, dann ist  erwartungstreu für F und die Varianz ist durch
erwartungstreu für F und die Varianz ist durch  gegeben. Je „dynamischer“ die Transportganglinie ist, desto ungenauer ist die Schätzung. Deshalb ist es sinnvoll, vorab eine Einteilung in Messintervalle (genannt Schichten)
gegeben. Je „dynamischer“ die Transportganglinie ist, desto ungenauer ist die Schätzung. Deshalb ist es sinnvoll, vorab eine Einteilung in Messintervalle (genannt Schichten)  so vorzunehmen, dass innerhalb eines Teilintervalls die Transportganglinie möglichst wenig schwankt. Dann werden unabhängig in jedem Teilintervall jeweils
so vorzunehmen, dass innerhalb eines Teilintervalls die Transportganglinie möglichst wenig schwankt. Dann werden unabhängig in jedem Teilintervall jeweils  Zeitpunkte mit
Zeitpunkte mit  rein zufällig für die Probennahmen bestimmt. Der Schätzer
rein zufällig für die Probennahmen bestimmt. Der Schätzer  ist dann nach wie vor erwartungstreu und nunmehr ist die Varianz gegeben durch
ist dann nach wie vor erwartungstreu und nunmehr ist die Varianz gegeben durch  . Für kleine Teilintervallvarianzen
. Für kleine Teilintervallvarianzen  wird die Schätzunsicherheit gegenüber der reinen Zufallsauswahl verringert. Aber auch diese geschichtete Zeitstichprobe ist stoffabhängig und damit schwierig in die Praxis umzusetzen. Für Stoffe, die stark abflussabhängig sind, sollte demnach in niederschlagsreichen Zeiten dichter als in niederschlagsarmen Zeiten beprobt werden.
wird die Schätzunsicherheit gegenüber der reinen Zufallsauswahl verringert. Aber auch diese geschichtete Zeitstichprobe ist stoffabhängig und damit schwierig in die Praxis umzusetzen. Für Stoffe, die stark abflussabhängig sind, sollte demnach in niederschlagsreichen Zeiten dichter als in niederschlagsarmen Zeiten beprobt werden.
Von besonderem Interesse ist hier die bevorzugt verwendete systematische Zeitstichprobe. Der erste Zeitpunkt  ist aus
ist aus  rein zufällig ausgewählt. Die übrigen Zeitpunkte
rein zufällig ausgewählt. Die übrigen Zeitpunkte  werden dann stets im gleichen Abstand aus den gleichlangen Teilintervallen
werden dann stets im gleichen Abstand aus den gleichlangen Teilintervallen  ausgewählt, d. h.
ausgewählt, d. h.  . Der auf das Gesamtintervall J hochgerechnete empirische Intervallmittelwert des Transports, also
. Der auf das Gesamtintervall J hochgerechnete empirische Intervallmittelwert des Transports, also

heißt Frachtschätzung aufgrund einer systematischen Zeitstichprobe. Auch dieser Schätzer ist erwartungstreu. Die Varianz und damit der mittlere quadratische Fehler ist durch  gegeben. Dabei bezeichnet
gegeben. Dabei bezeichnet  den Mittelwert aller
den Mittelwert aller  möglichen Messintervallvarianzen/Kovarianzen von T aus
möglichen Messintervallvarianzen/Kovarianzen von T aus  und
und  Um die Varianz, die näherungsweise der einer geschichteten Zeitstichprobe mit
Um die Varianz, die näherungsweise der einer geschichteten Zeitstichprobe mit  entspricht zu reduzieren, muss offenbar in Zeitintervallen höherer Dynamik von Konzentration bzw. Abfluss dichter als in Bereichen geringerer Dynamik beprobt werden. Als Faustregel könnte gelten, dass pro Abflusswelle mindestens zwei Proben erforderlich sind. Eine Verdopplung des Stichprobenumfangs halbiert in etwa die Varianz, wenn sich die Messintervallkovarianzen aufheben. Wenn nicht, kann sogar eine weitere Verbesserung aber auch eine Verschlechterung auftreten, je nach Vorzeichen der internen Kovarianz.
entspricht zu reduzieren, muss offenbar in Zeitintervallen höherer Dynamik von Konzentration bzw. Abfluss dichter als in Bereichen geringerer Dynamik beprobt werden. Als Faustregel könnte gelten, dass pro Abflusswelle mindestens zwei Proben erforderlich sind. Eine Verdopplung des Stichprobenumfangs halbiert in etwa die Varianz, wenn sich die Messintervallkovarianzen aufheben. Wenn nicht, kann sogar eine weitere Verbesserung aber auch eine Verschlechterung auftreten, je nach Vorzeichen der internen Kovarianz.
Weitere Einzelheiten zu Stichproben in kontinuierlichen Grundgesamtheiten sind in Hebbel (2000) und Hebbel und Steuer (2001) zu finden.
4.3 Quasi-kontinuierliche Beprobung
Eine Beprobungsstrategie zur Frachtbestimmung heißt quasi-kontinuierlich, wenn in den Messintervallen  mindestens eine der Größen Konzentration C, Abfluss Q oder Transport T dort als konstant angesehen werden kann (im Vergleich zur Variation im Gesamtzeitraum). Die Intervallkovarianzen
mindestens eine der Größen Konzentration C, Abfluss Q oder Transport T dort als konstant angesehen werden kann (im Vergleich zur Variation im Gesamtzeitraum). Die Intervallkovarianzen  bzw. die Intervallvarianzen
bzw. die Intervallvarianzen  verschwinden, und folglich ist die Fracht F (nahezu) exakt durch
verschwinden, und folglich ist die Fracht F (nahezu) exakt durch  bzw.
bzw.  (nach Abschn. 4.1 und 4.2) berechenbar.
(nach Abschn. 4.1 und 4.2) berechenbar.
In diesem Fall gilt daher für die Fracht (mit sehr guter Näherung)

wobei  und
und  die (mittleren bzw. konstanten) Konzentrations- und Abflussdaten in
die (mittleren bzw. konstanten) Konzentrations- und Abflussdaten in  darstellen. Damit kann die quasi-kontinuierliche Beprobung sowohl als Misch- als auch als Stichprobe angesehen werden.
darstellen. Damit kann die quasi-kontinuierliche Beprobung sowohl als Misch- als auch als Stichprobe angesehen werden.
Bei der Berechnung von Jahresfrachten mit der Jahreslänge  d und d
d und d  gelten stündliche Beobachtungen (Mischproben oder Punktproben) als quasi-kontinuierlich. Die Frachtermittlung aus den vorliegenden Daten ist (fast) fehlerfrei. Anders ist die Situation bei täglichen Probennahmen. Im Verlauf eines Tages
gelten stündliche Beobachtungen (Mischproben oder Punktproben) als quasi-kontinuierlich. Die Frachtermittlung aus den vorliegenden Daten ist (fast) fehlerfrei. Anders ist die Situation bei täglichen Probennahmen. Im Verlauf eines Tages  werden die Größen C, Q oder T nicht mehr konstant sein. Vielmehr muss mit größerer Dynamik und bei bestimmten Stoffen mit typischen periodischen Tagesschwankungen gerechnet werden, siehe dazu Symader (1988) und Symader und Strunk (1991). Für Tagesdaten (Mischproben
werden die Größen C, Q oder T nicht mehr konstant sein. Vielmehr muss mit größerer Dynamik und bei bestimmten Stoffen mit typischen periodischen Tagesschwankungen gerechnet werden, siehe dazu Symader (1988) und Symader und Strunk (1991). Für Tagesdaten (Mischproben  ,
,  oder Punktproben
oder Punktproben  haben Hebbel und Steuer (2007) gezeigt, dass die Frachtberechnung nach
haben Hebbel und Steuer (2007) gezeigt, dass die Frachtberechnung nach  über einen längeren Zeitraum (von mehreren Monaten) dennoch sehr genau ist. Die Einzelfehler heben sich weitgehend auf, sodass der Gesamtfehler der Fracht im Allgemeinen im Promillebereich liegt. Werden an einem Tag Einzelproben zu einem Zeitpunkt
über einen längeren Zeitraum (von mehreren Monaten) dennoch sehr genau ist. Die Einzelfehler heben sich weitgehend auf, sodass der Gesamtfehler der Fracht im Allgemeinen im Promillebereich liegt. Werden an einem Tag Einzelproben zu einem Zeitpunkt  genommen, dann ist darauf zu achten, dass sie möglichst „repräsentativ“ für den jeweiligen Tag im Sinne des Tagesmittelwertes sind. Insbesondere sollte also nicht bei extremen Tagessituationen untersucht werden. Zumindest sollten die Uhrzeiten der Beprobungen, d. h. die Routenplanungen, von Tag zu Tag wechseln.
genommen, dann ist darauf zu achten, dass sie möglichst „repräsentativ“ für den jeweiligen Tag im Sinne des Tagesmittelwertes sind. Insbesondere sollte also nicht bei extremen Tagessituationen untersucht werden. Zumindest sollten die Uhrzeiten der Beprobungen, d. h. die Routenplanungen, von Tag zu Tag wechseln.
5 Frachtermittlung bei Vorinformation
Bei der Mischprobenstrategie werden (quasi-)kontinuierlich beobachtete Abflussdaten benötigt. Daher ist ein Vergleich mit der Stichprobenstrategie nur dann geeignet, wenn dieselbe Information über den Abfluss genutzt wird. Im Folgenden werden daher systematisch erhobene Konzentrationswerte  und als „Vorinformation“ (quasi-)kontinuierlich aufgezeichnete Einflussgrößen, insbesondere die Abflussdaten
und als „Vorinformation“ (quasi-)kontinuierlich aufgezeichnete Einflussgrößen, insbesondere die Abflussdaten  vorausgesetzt, die auch zur Modellbildung herangezogen werden können (Abschn. 5.2).
vorausgesetzt, die auch zur Modellbildung herangezogen werden können (Abschn. 5.2).
5.1 Nicht-modellbasierte Frachtschätzer
Die nicht-modellbasierten Frachtschätzer stellen eine Modifikation des Stichprobenschätzers  unter Nutzung kontinuierlicher Abflusswerte dar. Nachfolgend werden die vier wichtigsten Schätzer vorgestellt und miteinander verglichen.
unter Nutzung kontinuierlicher Abflusswerte dar. Nachfolgend werden die vier wichtigsten Schätzer vorgestellt und miteinander verglichen.
Schätzer 1 Aus der Fracht  mit der Darstellung
mit der Darstellung  , vgl. theoretische Intervallkovarianz in Kap. 2, ergibt sich der so genannte Momentenschätzer
, vgl. theoretische Intervallkovarianz in Kap. 2, ergibt sich der so genannte Momentenschätzer

indem der theoretische Mittelwert  durch den empirischen Mittelwert
durch den empirischen Mittelwert  und die theoretische Kovarianz
und die theoretische Kovarianz  durch die empirische Kovarianz
durch die empirische Kovarianz  ersetzt wird. Die Umformung (nach dem zweiten Gleichheitszeichen) folgt aus dem Stichprobenschätzer
ersetzt wird. Die Umformung (nach dem zweiten Gleichheitszeichen) folgt aus dem Stichprobenschätzer  und zeigt, dass der „einfache“ Schätzer
und zeigt, dass der „einfache“ Schätzer  dann korrigiert wird, wenn die systematische Stichprobe den Abflussmittelwert
dann korrigiert wird, wenn die systematische Stichprobe den Abflussmittelwert  nicht richtig erfasst. Für
nicht richtig erfasst. Für  erfolgt eine Korrektur nach oben, bei
erfolgt eine Korrektur nach oben, bei  nach unten.
nach unten.
Schätzer 2 Der Frachtschätzer

ergibt sich aus  wenn statt der Einzelwerte
wenn statt der Einzelwerte  aus
aus  die theoretischen Mittelwerte
die theoretischen Mittelwerte  verwendet werden. Er ist erwartungstreu für
verwendet werden. Er ist erwartungstreu für  , da
, da  gilt (vgl. Hebbel 2006), und damit verzerrt für die eigentlich gesuchte Fracht F. Statistisch gesehen ist dieser Schätzer für die Fracht F folglich stets schlechter als
gilt (vgl. Hebbel 2006), und damit verzerrt für die eigentlich gesuchte Fracht F. Statistisch gesehen ist dieser Schätzer für die Fracht F folglich stets schlechter als  (im Vergleich der mittleren quadratischen Fehler), weil zu dem Quadrat der Verzerrung noch die Varianz des Schätzers hinzukommt.
(im Vergleich der mittleren quadratischen Fehler), weil zu dem Quadrat der Verzerrung noch die Varianz des Schätzers hinzukommt.
Schätzer 3 Werden in  die Einzelwerte
die Einzelwerte  aus
aus  durch den theoretischen Mittelwert
durch den theoretischen Mittelwert  ersetzt, entsteht der Schätzer
ersetzt, entsteht der Schätzer

Wegen  ist dieser Schätzer erwartungstreu für M und somit ebenfalls verzerrt für F und die Varianz liegt in der gleichen Größenordnung wie die von
ist dieser Schätzer erwartungstreu für M und somit ebenfalls verzerrt für F und die Varianz liegt in der gleichen Größenordnung wie die von  . Da nach dem Abschn. 4.1 in der Regel
. Da nach dem Abschn. 4.1 in der Regel  zwischen F und M liegt, ist
zwischen F und M liegt, ist  meist noch schlechter als
meist noch schlechter als  .
.
Schätzer 4 Die lineare Interpolation

und t aus einem Teilintervall  zwischen
zwischen  und
und  (bei geeigneter Extrapolation am Anfang und Ende) führt zu dem Schätzer
(bei geeigneter Extrapolation am Anfang und Ende) führt zu dem Schätzer

Hierbei ist  (in etwa) die Kovarianz von t und Q in
(in etwa) die Kovarianz von t und Q in  also ein Maß für ihren linearen Zusammenhang. Da aber Q im Allgemeinen keinen linearen Trend mit der Zeit t in
also ein Maß für ihren linearen Zusammenhang. Da aber Q im Allgemeinen keinen linearen Trend mit der Zeit t in  aufweist bzw. sich die linearen Trends im (gewichteten) Mittel aufheben, ist der zweite Summand annähernd Null, so dass die lineare Interpolationsmethode (im Wesentlichen) mit dem Schätzer 2 äquivalent ist.
aufweist bzw. sich die linearen Trends im (gewichteten) Mittel aufheben, ist der zweite Summand annähernd Null, so dass die lineare Interpolationsmethode (im Wesentlichen) mit dem Schätzer 2 äquivalent ist.
Zusammenfassung Da die Schätzer 2, 3 und 4 (in der Regel) statistisch schlechter als  sind, werden sie im Folgenden nicht weiter betrachtet.
sind, werden sie im Folgenden nicht weiter betrachtet.
5.2 Modellbasierte Frachtschätzer
Der Ansatz besteht darin, Modelle für die Konzentration bzw. den Transport der Art

bzw.

mit den Nebenbedingungen

zu entwickeln, deren Einflussgrößen  bzw.
bzw.  quasi-kontinuierlich beobachtet vorliegen. Dabei sind U und V nicht beobachtbare Restgrößen. Die Nebenbedingungen stellen sicher, dass die Fracht darstellbar ist in der Form
quasi-kontinuierlich beobachtet vorliegen. Dabei sind U und V nicht beobachtbare Restgrößen. Die Nebenbedingungen stellen sicher, dass die Fracht darstellbar ist in der Form

bzw.

d. h. statt der Originalwerte  bzw.
bzw.  können ebenso gut die Modellwerte
können ebenso gut die Modellwerte  bzw.
bzw.  für die Frachtberechnung verwendet werden, die aufgrund der gemeinsamen Beobachtungen von Einfluss- und Zielgrößen zu den Beobachtungszeitpunkten
für die Frachtberechnung verwendet werden, die aufgrund der gemeinsamen Beobachtungen von Einfluss- und Zielgrößen zu den Beobachtungszeitpunkten  geschätzt werden, z. B. mit der Methode der kleinsten Quadrate oder einem anderen Modellanpassungskriterium.
geschätzt werden, z. B. mit der Methode der kleinsten Quadrate oder einem anderen Modellanpassungskriterium.
Üblich ist in diesem Zusammenhang die Verwendung reiner C-Q-Modelle wie beispielsweise

oder

bzw. eine Kombination beider Ansätze, um sowohl einen Anstiegs- als auch Verdünnungseffekt in C bei wachsendem Q zu beschreiben, siehe etwa Steinebach (1994), Keller et al. (1997) und Brunswig (2000). Weist  in J einen periodischen Verlauf auf, dann könnte die Hinzunahme der trigonometrischen Schwingungen
in J einen periodischen Verlauf auf, dann könnte die Hinzunahme der trigonometrischen Schwingungen  und ggf. einiger Oberwellen nützlich sein, vgl. beispielsweise Uhlig und Kuhbier (2001a, b). Wird durch den Inhaltsstoff C im Wesentlichen die Leitfähigkeit
und ggf. einiger Oberwellen nützlich sein, vgl. beispielsweise Uhlig und Kuhbier (2001a, b). Wird durch den Inhaltsstoff C im Wesentlichen die Leitfähigkeit  bewirkt, die (quasi-)kontinuierlich beobachtet wird, dann ist es sinnvoll,
bewirkt, die (quasi-)kontinuierlich beobachtet wird, dann ist es sinnvoll,  als eine Einflussgröße im Modell zu berücksichtigen, vgl. spätere Beispielrechnungen.
als eine Einflussgröße im Modell zu berücksichtigen, vgl. spätere Beispielrechnungen.
Da in der Praxis jede Funktion (lokal) linear approximierbar ist, kann ohne große Einschränkung ein sogenanntes lineares Modell, geschrieben als Zustandsgleichung

bzw.

mit den obigen Nebenbedingungen gewählt werden. Für die Beobachtungszeitpunkte  ergeben sich die entsprechenden sogenannten Beobachtungsgleichungen, aus denen die Koeffizienten geschätzt werden.
ergeben sich die entsprechenden sogenannten Beobachtungsgleichungen, aus denen die Koeffizienten geschätzt werden.
Die Einflussgrößen selbst können dabei auch nichtlineare Transformationen anderer Größen sein, beispielsweise vom Abfluss  der Art
der Art

Dennoch gelten Modelle mit derart transformierten Einflussgrößen als linear (in den Koeffizienten). Aus der statistischen Theorie der linearen Modelle und ihren Kleinst-Quadrate-Schätzungen können folgende Aussagen abgeleitet werden, siehe auch Hebbel und Steuer (2007) (Abschn. 4.2):
-
1.
Die C- und T-Modelle sind zwar äquivalent, weil sie durch Multiplikation bzw. Division mit Q ineinander überführbar sind. Jedoch sind die Kleinst-Quadrate-Schätzer nicht identisch, da unterschiedliche Restquadratsummen minimiert werden.
-
2.
Sind in dem linearen Modell für die Konzentration C als Einflussgrößen ein Absolutglied (
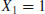 ) und der Abfluss (
) und der Abfluss ( ) enthalten, dann werden für die (exakte) Berechnung der Fracht
) enthalten, dann werden für die (exakte) Berechnung der Fracht 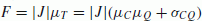 über die Zustandsgleichung die übrigen Einflussgrößen gar nicht benötigt. Die betreffenden Koeffizienten verschwinden. Bereits bei der Diskussion der theoretischen Begriffe Fracht und Mischprobenfracht in Kap. 3 hatte sich gezeigt, dass nur der lineare Zusammenhang zwischen C und Q eine Rolle spielt. Diese Erkenntnis setzt sich hier fort. Bei der Schätzung der Fracht aus den Beobachtungsgleichungen hingegen entfallen die weiteren Einflussgrößen nicht, vgl. Aussage 4.
über die Zustandsgleichung die übrigen Einflussgrößen gar nicht benötigt. Die betreffenden Koeffizienten verschwinden. Bereits bei der Diskussion der theoretischen Begriffe Fracht und Mischprobenfracht in Kap. 3 hatte sich gezeigt, dass nur der lineare Zusammenhang zwischen C und Q eine Rolle spielt. Diese Erkenntnis setzt sich hier fort. Bei der Schätzung der Fracht aus den Beobachtungsgleichungen hingegen entfallen die weiteren Einflussgrößen nicht, vgl. Aussage 4. -
3.
Ein „sparsames“ Modell mit wenigen aber wichtigen Einflussgrößen ist oft besser als ein großes komplexes Modell mit vielen, teilweise unwesentlichen Einflussgrößen und dafür zwar einer etwas geringeren Restvarianz. In einem Modell mit sehr vielen Regressoren können die geschätzten Koeffizienten größere Varianzen/Kovarianzen aufweisen, die die kleinere Restvarianz überkompensieren und somit in der Frachtschätzung insgesamt zu einem deutlich größeren mittleren quadratischen Fehler führen.
-
4.
Der Vorteil linearer Modelle besteht darin, dass die Schätzung aufgrund der Beobachtungsgleichungen zu den Zeitpunkten
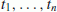 nach der Methode der kleinsten Quadrate unter den angegebenen Restriktionen (Index r) geschlossen angegegeben werden kann.
nach der Methode der kleinsten Quadrate unter den angegebenen Restriktionen (Index r) geschlossen angegegeben werden kann.
Schätzer 5 Im C-Modell mit Absolutglied ergibt sich für die Fracht der (restringierte) Schätzer

mit

Es sind  der Vektor der Einflussvariablen,
der Vektor der Einflussvariablen,  bzw.
bzw.  der Vektor ihrer empirischen bzw. theoretischen Intervallmittelwerte,
der Vektor ihrer empirischen bzw. theoretischen Intervallmittelwerte,  die Matrix ihrer empirischen Intervallvarianzen/Kovarianzen und
die Matrix ihrer empirischen Intervallvarianzen/Kovarianzen und  bzw.
bzw.  der Vektor der empirischen bzw. theoretischen Intervallkovarianzen der Einflussgrößen und Q usw. Der hochgestellte Strich bedeutet das Transponiertzeichen für Vektoren und Matrizen.
der Vektor der empirischen bzw. theoretischen Intervallkovarianzen der Einflussgrößen und Q usw. Der hochgestellte Strich bedeutet das Transponiertzeichen für Vektoren und Matrizen.
Besteht  nur aus einer Einflussgröße X, dann kürzen sich die meisten Werte und es verbleibt
nur aus einer Einflussgröße X, dann kürzen sich die meisten Werte und es verbleibt  , vgl. Schätzer 5a mit
, vgl. Schätzer 5a mit  .
.
Im Spezialfall, dass eine der Einflussgrößen neben dem Absolutglied der Abfluss Q ist, ergibt sich die Vereinfachung  .
.
Der einfache Stichprobenschätzer  wird durch den Zusatzterm „korrigiert“, wenn die Stichprobe sowohl die Intervallmittelwerte von Q und der Einflussgrößen
wird durch den Zusatzterm „korrigiert“, wenn die Stichprobe sowohl die Intervallmittelwerte von Q und der Einflussgrößen  als auch die Kovarianzen von
als auch die Kovarianzen von  und Q nicht richtig erfasst. Die Richtung der Korrektur wird dabei durch die jeweiligen Vorzeichen bestimmt.
und Q nicht richtig erfasst. Die Richtung der Korrektur wird dabei durch die jeweiligen Vorzeichen bestimmt.
Schätzer 5a Ist im Schätzer 5 der Abfluss Q die einzige Einflussvariable, dann gilt für den sogenannten Regressionsschätzer

Der Schätzer  kann damit auch approximativ als ein Schätzer in einem linearen C-Q-Modell angesehen werden. Der Unterschied besteht darin, dass zusätzlich eine Korrektur von
kann damit auch approximativ als ein Schätzer in einem linearen C-Q-Modell angesehen werden. Der Unterschied besteht darin, dass zusätzlich eine Korrektur von  erfolgt, wenn die Stichprobe auch die Intervallvarianz von Q nicht richtig erfasst. Enthält die Ganglinie von Q zahlreiche Extremwerte (Hochwasser, Niedrigwasser), so wird die Stichprobenvarianz von Q sehr schwanken und die Folge können „Überkorrekturen“ sein. Daher empfielt sich der Schätzer 1 als robuste Variante des Schätzers 5a.
erfolgt, wenn die Stichprobe auch die Intervallvarianz von Q nicht richtig erfasst. Enthält die Ganglinie von Q zahlreiche Extremwerte (Hochwasser, Niedrigwasser), so wird die Stichprobenvarianz von Q sehr schwanken und die Folge können „Überkorrekturen“ sein. Daher empfielt sich der Schätzer 1 als robuste Variante des Schätzers 5a.
Schätzer 6 Im T-Modell gilt für den (restringierten) Frachtschätzer

mit

Die Bezeichnungen sind analog zum C-Modell gewählt und die Interpretation des Schätzers ist entsprechend.
Schätzer 6a Enthält das Modell als einzige Einflussgröße den Abfluss, d. h. ist  , dann gilt
, dann gilt

und damit (wegen  )
)

Das Resultat ist ein so genannter Verhältnisschätzer und wird von OSPAR in den (RID) Principles empfohlen, siehe INPUT (2000).
Schätzer 7 Ist ein Absolutglied vorhanden und wird das T-Modell in der Form  geschrieben, dann vereinfacht sich der Frachtschätzer zu
geschrieben, dann vereinfacht sich der Frachtschätzer zu

Schätzer 7a Ist überdies  , so folgt speziell
, so folgt speziell

Die Wahl eines Absolutglieds im T-Modell sollte sorgfältig überlegt werden. Im analogen C-Modell wäre die entsprechende Einflussgröße  , d. h. das Absolutglied im T-Modell ist nur dann sinnvoll, wenn ein gleichbleibender „Verdünnungseffekt“ umgekehrt proportional zum Abfluss zu erwarten ist bzw. wenn stets ein „Grundtransport“ vorhanden ist.
, d. h. das Absolutglied im T-Modell ist nur dann sinnvoll, wenn ein gleichbleibender „Verdünnungseffekt“ umgekehrt proportional zum Abfluss zu erwarten ist bzw. wenn stets ein „Grundtransport“ vorhanden ist.
Zusammenfassung Wenn es die Datenlage zulässt, sollte ein „stetigkeitskorrigierender“ Frachtschätzer verwendet werden. Unproblematisch und in der Güte vergleichbar sind der Momentenschätzer 1, der Regressionsschätzer 5a und der Verhältnisschätzer 6a, die in der Regel bessere Ergebnisse liefern als der einfache Stichprobenschätzer  . Der Schätzer 7a ist nur in Ausnahmefällen brauchbar. Weitergehende Modellschätzer 5 oder 7 müssen sachlogisch sehr gut begründet sein und die Konzentrations- bzw. Transportganglinie nahezu exakt beschreiben. Modelle, die sich lediglich an einer „guten“ Datenanpassung orientieren, sind mit Vorsicht zu beurteilen.
. Der Schätzer 7a ist nur in Ausnahmefällen brauchbar. Weitergehende Modellschätzer 5 oder 7 müssen sachlogisch sehr gut begründet sein und die Konzentrations- bzw. Transportganglinie nahezu exakt beschreiben. Modelle, die sich lediglich an einer „guten“ Datenanpassung orientieren, sind mit Vorsicht zu beurteilen.
6 Beispielrechnungen
Zur Veranschaulichung der Aussagen des Kap. 5 werden vier typische Beispiele ausgewählt. Zahlreiche weitere sind in Hebbel und Steuer (2007) zu finden. Für die empirischen Berechnungen werden wegen der einfacheren Unterteilung nur Intervalle der Länge von 364 Tagen herangezogen. Die Konzentrationsdaten C und die Abflussdaten Q sind quasi-kontinuierlich als Tagesdaten (Tagesmischproben oder Tagesstichproben) verfügbar. Nach der Diskussion im Kap. 4 ist damit die Gesamtfracht F im 364-Tageintervall, kurz Jahresfracht genannt, (fast) fehlerfrei berechenbar und dient als Referenzwert. Die Mischprobenfracht M wird zur Veranschaulichung der Fundamentalgleichung aus Kap. 3 ebenfalls angegeben.
Als Stichprobenstrategien werden die 14-tägige Mischprobe  , die einen Wert liefert, der meist zwischen F und M liegt, und die 14-tägige systematische Stichprobe
, die einen Wert liefert, der meist zwischen F und M liegt, und die 14-tägige systematische Stichprobe  bezüglich der Konzentration C gewählt, und zwar für Chlorid Cl in Bimmen (Rhein) und Nitrat NO3 in Palzem (Mosel), jeweils für zwei verschiedene Jahre. Die Mischprobe
bezüglich der Konzentration C gewählt, und zwar für Chlorid Cl in Bimmen (Rhein) und Nitrat NO3 in Palzem (Mosel), jeweils für zwei verschiedene Jahre. Die Mischprobe  wird mathematisch (als Mittelwert über jeweils 14-Tagesintervalle) bestimmt und ist somit frei von sämtlichen übrigen Fehlern (vgl. Abschn. 4.1). Die 14 verschieden Werte für
wird mathematisch (als Mittelwert über jeweils 14-Tagesintervalle) bestimmt und ist somit frei von sämtlichen übrigen Fehlern (vgl. Abschn. 4.1). Die 14 verschieden Werte für  sind als Liniengrafik dargestellt und schwanken (wegen der Erwartungstreue) um F. Die Schwankungsintensität bestimmt die Varianz des Schätzers
sind als Liniengrafik dargestellt und schwanken (wegen der Erwartungstreue) um F. Die Schwankungsintensität bestimmt die Varianz des Schätzers  Alle diese Werte sind zu Vergleichszwecken mit den „stetigkeitskorrigierenden“ Frachtschätzern in die Bilder eingetragen.
Alle diese Werte sind zu Vergleichszwecken mit den „stetigkeitskorrigierenden“ Frachtschätzern in die Bilder eingetragen.
In die Berechnungen einbezogen werden die C-Modellschätzer 1 und 5a, ein Modellschätzer 5 für Chlorid Cl in Abhängigkeit der Leitfähigkeit LF sowie die T-Modellschätzer 6a und 7a (Abb. 1–4).
Kommentare
Cl Die Ganglinien von Cl weisen einen deutlichen Wochengang auf, ebenso wie die Leitfähigkeit LF mit sehr ähnlichen Verläufen. Insbesondere 1980 überträgt sich der Wochengang auf die Schätzwerte  Hier ist der Cl-LF-Modellschätzer besonders gut. 1979 schneiden Momenten- und Verhältnischätzer 1 und 6a am besten ab und sind auch besser als
Hier ist der Cl-LF-Modellschätzer besonders gut. 1979 schneiden Momenten- und Verhältnischätzer 1 und 6a am besten ab und sind auch besser als  . Schätzer 7a deckt sich mit
. Schätzer 7a deckt sich mit  . Die Vorteile relativieren sich im Folgejahr 1980. Selbst stoffbezogen sind also keine generellen Aussagen zur Verwendung eines bestimmten Schätzers möglich.
. Die Vorteile relativieren sich im Folgejahr 1980. Selbst stoffbezogen sind also keine generellen Aussagen zur Verwendung eines bestimmten Schätzers möglich.
NO3 Momenten- und Verhältnischätzer sind deutlich besser als  , am besten ist jedoch
, am besten ist jedoch  (gering verzerrt), zumindest für 1980. Schätzer 7a ist ganz schlecht und gar nicht erst eingetragen (weil C nicht umgekehrt proportional zu Q ist).
(gering verzerrt), zumindest für 1980. Schätzer 7a ist ganz schlecht und gar nicht erst eingetragen (weil C nicht umgekehrt proportional zu Q ist).
1981 ist ein Beispiel dafür, dass  nicht zwischen F und M liegen muss (interne und externe Kovarianz haben verschiedene Vorzeichen).
nicht zwischen F und M liegen muss (interne und externe Kovarianz haben verschiedene Vorzeichen).
Literatur
BMU (Hrsg) (2004) Umweltpolitik. Die Wasserrahmenrichtlinie – Neues Fundament für den Gewässerschutz in Europa. Berlin im September 2004: Bundesministerium für Umwelt, Naturschutz und Reaktorsicherheit
BMU (Hrsg) (2005) Umweltpolitik. Die Wasserrahmenrichtlinie – Ergebnisse der Bestandsaufnahme 2004 in Deutschland. Berlin im August 2005: Bundesministerium für Umwelt, Naturschutz und Reaktorsicherheit
Brunswig D (2000) Die Immissionsanalyse gewässerkundlicher Monitoringdaten mit dem Simulationsmodell Transpos: Frachtberechnung, Frachtnormierung und Trendanalyse. In: Fehr 2000:159–201
DiToro DM (1984) Probability model of stream quality due to runoff. J Environ Enginrg 110(3):607–628
Förstner U, Westrich B (2005) BMBF coordinated research project SEDYMO (2002–2006). Sediment dynamics and pollutant mobility in river basins. J Soils Sediments 5(3):134–138
Fehr G (Hrsg) (2000) Nährstoffbilanzen für Flußeinzugsgebiete. Ein Beitrag zur Umsetzung der EU-Wasserrahmenrichtlinie. Vieweg, Wiesbaden
Gölz E, Schmidt A (Projektleiter) (2003) Bedeutung der Nebenflüsse für den Feststoffhaushalt der Elbe – Abschlussbericht. Koblenz: Bundesanstalt für Gewässerkunde, BfG-1382
Hebbel H (2000) Theorie der Frachtberechnung und -standardisierung in der Wassergütewirtschaft – Entwurf von Zeitstichprobenplänen. Discussion Papers. In: Hauptmann H, Krumbholz W (eds) Statistics and Quantitative Economics No 91. Universität der Bundeswehr Hamburg
Hebbel H (2006) Die systematische Stichprobe zur Schätzung zweiter Momente in kontinuierlichen Grundgesamtheiten. Discussion Papers. In: Hauptmann H, Krumbholz W (eds) Statistics and Quantitative Economics No 118. Universität der Bundeswehr Hamburg
Hebbel H, Steuer D (2001) Sampling for continuous (space-time) processes. Mathematical Statistics with Applications in Biometry. In: Kunert J, Trenkler G (eds) Festschrift in Honour of Prof. Dr. Siegfried Schach. Lohmar, Köln, pp 277–291
Hebbel H, Steuer D (2007) Empirische Untersuchungen zur Berechnung von Frachten in Fließgewässern. In: Hauptmann H, Krumbholz W (eds) Statistics and Quantitative Economics No 120, Discussion Papers. Universität der Bundeswehr Hamburg, Hamburg
Heininger P, Schild R et al. (2002a) Ermittlung der gewässerseitigen Einträge von polyzyklischen aromatischen Kohlenwasserstoffen (PAKs) in die Nordsee auf der Basis einer harmonisierten Methodik (internationales Pilotprojekt). Umweltbundesamt, Berlin (Texte 56/02, UBA-FB 000343)
Heininger P, Schild R et al. (2002b) International pilot study for the determination of riverine inputs of polycyclic aromatic hydrocarbons (PAHs) to the maritime atea on the basis of a harmonised methodology – Final Report. Umweltbundesamt, Berlin (Texte 57/02, UBAFB 000343e)
Hilden M (Bearbeiter) (2003) Ermittlung von Stofffrachten in Fließgewässern – Probenahmestrategien und Berechnungsverfahren. In: Länderarbeitsgemeinschaft Wasser LAWA. Kulturbuch-Verlag, Berlin
INPUT (2000) The comprehensive study on riverine inputs – (RID) Principles. Lisbon 17–21 January: INPUT 00/7/info.1-E
Keller M, Hilden M, Joost M (1997) Vergleich von Schätzmethoden für jährliche Stofffrachten am Beispiel des IKSR-Meßprogrammes 1995. Bundesanstalt für Gewässerkunde, Koblenz (BfG-1078)
Klopp R (1986) Über die Ermittlung von Frachten in Fließgewässern. Wasser 66:149–158
Richards RP (1998) Estimation of pollutant loads in rivers and streams: A guidance document for NPS Programs. Project Report prepared under Grant X998397-01-0, U.S. Environmental Protection Agency, Region VIII, Denver
Schreiber W, Krauß-Kalweit I (1999) Frachten von Wasserinhaltsstoffen in Fließgewässern – Einfluß der Probenahmestrategie auf die Ermittlung. Wasserwirtschaft 89:520–529
Steinebach G (1994) Zur Ermittlung von jährlichen Stofffrachten in großen Fließgewässern am Beispiel der IKSR-Zahlentafeln. Bundesanstalt für Gewässerkunde, Koblenz (BfG-0827)
Symader W (1988) Zur Problematik der Frachtermittlung. Wasser 71:145–161
Symader W, Strunk N (1991) Die zeitliche Dynamik des Schwebstofftransports und seine Bedeutung für die Gewässerbeschaffenheit. Wasser 77:159–169
Trepel M, Kluge W (2002) Eignung von Modellen für die Umsetzung der EU-Wasserrahmenrichtlinie in Schleswig-Holstein. Endbericht für Landesamt für Natur und Umwelt des Landes Schleswig-Holstein, Abt. Gewässergüte. Ökologie-Zentrum an der Christian-Albrechts-Universität zu Kiel, Kiel
Uhlig S, Kuhbier P (2001a) Methoden der Trendabschätzung zur Überprüfung von Reduktionszielen im Gewässerschutz. Umweltbundesamt, Berlin (Texte 49/01, UBA-FB 00204)
Uhlig S, Kuhbier P (2001b) Trend methods for the assessment of effectiveness of reduction measures in the water system. Federal Environmental Agency (Umweltbundesamt), Berlin (Texte 80/01, UBA-FB 00204/e)
Warn AE, Brew JS (1980) Mass balance. Wat Res 14(7):1427–1434
Westrich BJ, Förstner U (2005) Sediment dynamics and pollutant mobility in rivers (SEDYMO): assessing catchment-wide emission-immission relationships from sediment studies. BMBF coordinated research project SEDYMO (2002–2006). J Soils Sediments 5(4):197–200
Danksagung
Für sehr viele wertvolle Hinweise und Anregungen danke ich dem Arbeitskreis Chemometrie im UA1 des DIN NAW/A1, insbesondere Herrn Dr. Neitzel und Herrn Dr. v. Tümpling sowie den Referenten.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Hebbel, H. Analyse „stetigkeitsbasierter“ Methoden zur Bestimmung von Stofffrachten in Fließgewässern. Environ Sci Eur 21, 527–538 (2009). https://doi.org/10.1007/s12302-009-0085-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s12302-009-0085-x
Schlüsselwörter
- Frachtberechnung
- Gewässergüte
- Mittlerer quadratischer Fehler
- Schadstoffe
- Statistische Modelle
- Systematische Stichprobe
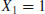 ) und der Abfluss (
) und der Abfluss ( ) enthalten, dann werden für die (exakte) Berechnung der Fracht
) enthalten, dann werden für die (exakte) Berechnung der Fracht 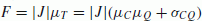 über die Zustandsgleichung die übrigen Einflussgrößen gar nicht benötigt. Die betreffenden Koeffizienten verschwinden. Bereits bei der Diskussion der theoretischen Begriffe Fracht und Mischprobenfracht in Kap. 3 hatte sich gezeigt, dass nur der lineare Zusammenhang zwischen C und Q eine Rolle spielt. Diese Erkenntnis setzt sich hier fort. Bei der Schätzung der Fracht aus den Beobachtungsgleichungen hingegen entfallen die weiteren Einflussgrößen nicht, vgl. Aussage 4.
über die Zustandsgleichung die übrigen Einflussgrößen gar nicht benötigt. Die betreffenden Koeffizienten verschwinden. Bereits bei der Diskussion der theoretischen Begriffe Fracht und Mischprobenfracht in Kap. 3 hatte sich gezeigt, dass nur der lineare Zusammenhang zwischen C und Q eine Rolle spielt. Diese Erkenntnis setzt sich hier fort. Bei der Schätzung der Fracht aus den Beobachtungsgleichungen hingegen entfallen die weiteren Einflussgrößen nicht, vgl. Aussage 4. 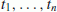 nach der Methode der kleinsten Quadrate unter den angegebenen Restriktionen (Index r) geschlossen angegegeben werden kann.
nach der Methode der kleinsten Quadrate unter den angegebenen Restriktionen (Index r) geschlossen angegegeben werden kann.
 in Palzem (Mosel) 1980, die Werte F—,
in Palzem (Mosel) 1980, die Werte F—,  - -, M ... und die 14 linear verbundenen Werte
- -, M ... und die 14 linear verbundenen Werte  — im Vergleich mit „stetigkeitsbasierten“ Frachtschätzern}
— im Vergleich mit „stetigkeitsbasierten“ Frachtschätzern}

 - -,
- -,  und die 14 linear verbundenen Werte
und die 14 linear verbundenen Werte  — im Vergleich mit „stetigkeitsbasierten“ Frachtschätzern
— im Vergleich mit „stetigkeitsbasierten“ Frachtschätzern
 in Bimmen (Rhein) 1980, die Werte F—,
in Bimmen (Rhein) 1980, die Werte F—,  - -,
- -,  und die 14 linear verbundenen Werte
und die 14 linear verbundenen Werte  — im Vergleich mit „stetigkeitsbasierten“ Frachtschätzern
— im Vergleich mit „stetigkeitsbasierten“ Frachtschätzern